Inscription
行来春色三分雨 睡去巫山一片云
Background
As we all know,gryz是一个永远都不会让你休息的地方,每天他都有你意想不
到的任务而你只能按照祂所吩咐的去做,否则你的德育积分就。。。
某一天, 的魔爪伸向61级,你要知道lyk是一个被周武王看重的学生
所以周武王会布置许多任务给他,那么lyk想他怎样忙里偷闲
去争取尽可能多的时间去休息,可他由于周武王繁重的任务没时间去想这些问题
所以他找到了你希望你可以帮助他
Description
每天起来,lyk都会积极地去周武王那里领取任务,每个任务由一个开始时刻与一个持续时间构成
他每天的待电时间为N分钟,当他拿到任务时就开始工作。但有时候周武王会
在同一时刻给他很多任务使他完全没有办法完全承受,所以周武王可怜他告诉
他:他可以选择其中一个来做,剩下的交给wpgwhpg来做。但是如果只有一个
任务在这一个时间段内,那么必须由他来完成。还有一种最极端的可能,那就是
他在专心做一项任务时,又来了新的任务,那么这个任务开始时间意味着与他现
在的任务时间冲突,那么这个新任务就还是交给wpgwhpg来做
如果某任务于第M分钟开始,持续时间为P分钟,则该任务将在第M + P − 1分钟结束。
想问你他需要怎样选任务,才能获得最多时间休息?
Input Output
Input
第一行两个整数N和K(K表示任务总数)
接下来有K行,每行有两个整数M和P
Output
仅一行,即他所获得的最小工作时间
Input Sample
15 6
1 2
1 6
4 11
8 7
8 2
11 5
Output Sample
13
Data Range
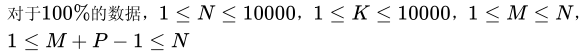
Code+Solution
/*这道题第一眼看的时候,设f[i]表示1--i的最大空闲时间
但是我们又可以发现,i时刻的最大空闲时间和后面选择任务的持续的时间是有关系的
那么我们就用f[i]来表是i——n的最大空闲时间,即倒着找
那么我们就可以推出两个状态转移方程式
(1):这一时刻没有任务,那么就在上一时刻的最大空闲时间+1:f[i]=f[i+1]+1
(2):这一时刻有任务,f[i]=max(f[i],f[i+s[q].t])s[q].t表示在这个时刻的任务的
持续时间,找出选择哪一个本时刻任务使空闲时间最大化
那么既然是倒着搜,从后往前的任务对应的开始时间自然也要反过来,从大到小
排序,在进行状态刷新的时候,q不断计一下已经到哪一个任务了*/
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 11000;
ll n,k,q=1;
ll a[N],f[N];
struct edge
{
ll p,t;
} s[N];
bool cmp(edge a,edge b)
{
return a.p>b.p;
}
int main()
{
memset(a,0,sizeof(a));
memset(f,0,sizeof(f));
cin>>n>>k;
for(int i=1; i<=k; i++)
{
cin>>s[i].p>>s[i].t;
a[s[i].p]++;
}
sort(s+1,s+k+1,cmp);//从大到小
for(ll i=n; i>0; i--)//倒着搜
{
if(a[i]==0)
f[i]=f[i+1]+1;//本时刻无任务
else
{
for(ll j=1; j<=a[i]; j++)
{
f[i]=max(f[i+s[q].t],f[i]);//本时刻有任务
q++;//不断记任务进度
}
}
}
cout<<n-f[1];//最后只需要把最大空闲时间与总时间做差即可
return 0;
}
/*15 6
2
6
11
7
2
5
13*/